Grounded Two-DOF System, Equation of Motion

Newton’s law can be applied to the system in Figure 1.1 to derive the equations of motion. The steps are omitted for brevity. The resulting pair of ordinary differential equations can be represented in matrix form and are coupled via the damping and stiffness matrices.

A shorthand form is

The matrices and vectors are

Consider the undamped, homogeneous form of equation (1.2).

Seek a harmonic solution of the form



The  vector is the generalized coordinate vector. The undamped, homogeneous equation is transformed through substitution and algebraic manipulation into the generalized eigenvalue problem.
vector is the generalized coordinate vector. The undamped, homogeneous equation is transformed through substitution and algebraic manipulation into the generalized eigenvalue problem.

TThe eigenvalues  can be found by setting the determinant equal to zero.
can be found by setting the determinant equal to zero.

There is an eigenvalue for each degree-of-freedom. Each angular natural frequency is then calculated from the square root of the respective eigenvalue. The corresponding eigenvectors represent orthogonal mode shapes. The eigenvector for each mode is found via

An eigenvector matrix 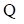 can be formed. The eigenvectors are inserted in column format.
can be formed. The eigenvectors are inserted in column format.

The coefficient 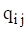 represents the modal displacement of mass i for mode j.
represents the modal displacement of mass i for mode j.
Each eigenvector can be multiplied by an arbitrary scale factor. A mass-normalized eigenvector matrix  can be calculated such that the following orthogonality relations are obtained.
can be calculated such that the following orthogonality relations are obtained.


The superscript T represents matrix transpose. The identity matrix is I, a diagonal matrix of ones. The diagonal matrix of eigenvalues Ω.
Grounded Two-DOF System Example, Free Vibration
Now define a modal coordinate  in terms of the normalized eigenvector matrix such that the displacement vector is
in terms of the normalized eigenvector matrix such that the displacement vector is

Substitute equation (3.1) into equation (1.2).

Premultiply by the transpose of the normalized eigenvector matrix.

The orthogonality relationships yield

Furthermore, the following simplifying assumption is made for the damping matrix.

The equation of motion can now be written as

The two equations are now uncoupled in terms of the modal coordinates. The modal displacement for free vibration response to initial conditions is found via Laplace transforms as shown in Reference [3]. The modal displacement for dof i is

The damped angular natural frequency is

The physical displacement can then be found by substituting equation (3.7) into (3.1). The physical displacements can be expressed in terms of the eigenvector coefficients and modal coordinates as
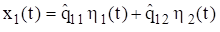

The modal displacement initial conditions are required for the complete solution. These can be found from the following transformations.


The participation factors and effective modal masses are indicators of how excitable the modes are given uniform base excitation to the given system. Some modes are more readily excited than others, and some cannot be excited at all for this excitation type.
The system’s generalized mass matrix  is given by
is given by

Again, the generalized mass will be the identity matrix if the eigenvectors are mass normalized. Let  be the influence vector which represents the displacements of the masses resulting from static application of a unit ground displacement. Define a coefficient vector
be the influence vector which represents the displacements of the masses resulting from static application of a unit ground displacement. Define a coefficient vector  as
as
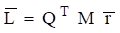
The modal participation factor matrix for mode i is 

The effective modal mass  for mode i is
for mode i is
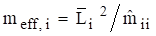
The system in Figure 5.1 has the following parameters.
| Variable | Value |
|---|---|
 |
2 lbm |
 |
1 lbm |
 |
150 lbf/in |
 |
100 lbf/in |
 |
0.01 in |
 |
0.005 in |
Assume 5% damping for each mode. The initial velocity is zero for each mass.
Apply the mass and stiffness values from Table 1.1 into equation (1.1) to form the following matrices.

The 1/386 factor is needed to convert lbm to lbf sec^2/in.
The eigenvalues and vectors are found by inserting these matrices into equations (2.5) and (2.6). The results are shown in the following table.
| Mode | Angular Natural Frequency (rad/sec) | Natural Frequency (Hz) | Participation Factor | Modal Mass Ratio |
|---|---|---|---|---|
| 1 | 125.25 | 20.0 | 0.085 | 0.935 |
| 2 | 266.72 | 42.5 | -0.022 | 0.065 |
The mass-normalized mode shapes in matrix format are
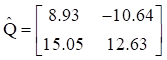
The response time histories for the initial conditions are shown in Figure 5.2.


Consider the system in the above figure. This system could represent a simple, two-node finite element model of a rod’s longitudinal vibration. A characteristic of this system is that the fundamental mode is a rigid-body mode at zero frequency. Both masses move in unison for the rigid-body mode. Newton’s law can be applied to the system to derive the equations of motion. The steps are omitted for brevity. The resulting pair of ordinary differential equations can be represented in matrix form.

The eigenvalues and vectors are found using the method shown in Section 6.1.2. Each angular natural frequency is then calculated from the square root of the respective eigenvalue.


The mass-normalized eigenvectors, representing the mode shapes, are

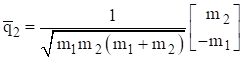
Again, the two masses move in unison for the first mode. They move 180 degrees-out-phase for the second mode. The semi-definite system is revisited in Section 12.3.3.
Consider the system in Figure 6.3 with the values in the following table.
| Variable | Value |
|---|---|
 |
2 lbm |
 |
1 lbm |
| k | 2000 lbf/in |
The mass and stiffness matrices are

The 1/386 factor is needed to convert lbm to lbf sec^2/in.
The eigenvalues and vectors are found by inserting these matrices into equations (2.5) and (2.6). The angular natural frequencies are


The mass-normalized eigenvectors in column format are
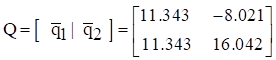
The total mass sum is 3 lbm (0.00777 lbf sec^2/in) which is also the effective modal mass of the rigid-body modes. The second mode has zero effective modal mass.



